管流验证

本案例依然在验证边界层的解析能力，但是与平板边界层有两点不同，其一是本案例为内流，而平板边界层为外流；其二是本案例有一个守恒关系，即管流压降和壁面阻力成正相关，因此可以通过该案例进一步验证粘性力和压力耦合是否正确解析。

计算域尺度

对于管流，其内部流动分为非充分发展段和充分发展段，进入充分发展段后，速度形态不在发生任何变化，如Figure.1所示。而此类问题存在的经验解或是实验都是针对充分发展段而言的，因此需要注意计算域必须延伸到充分发展段所在的区域。

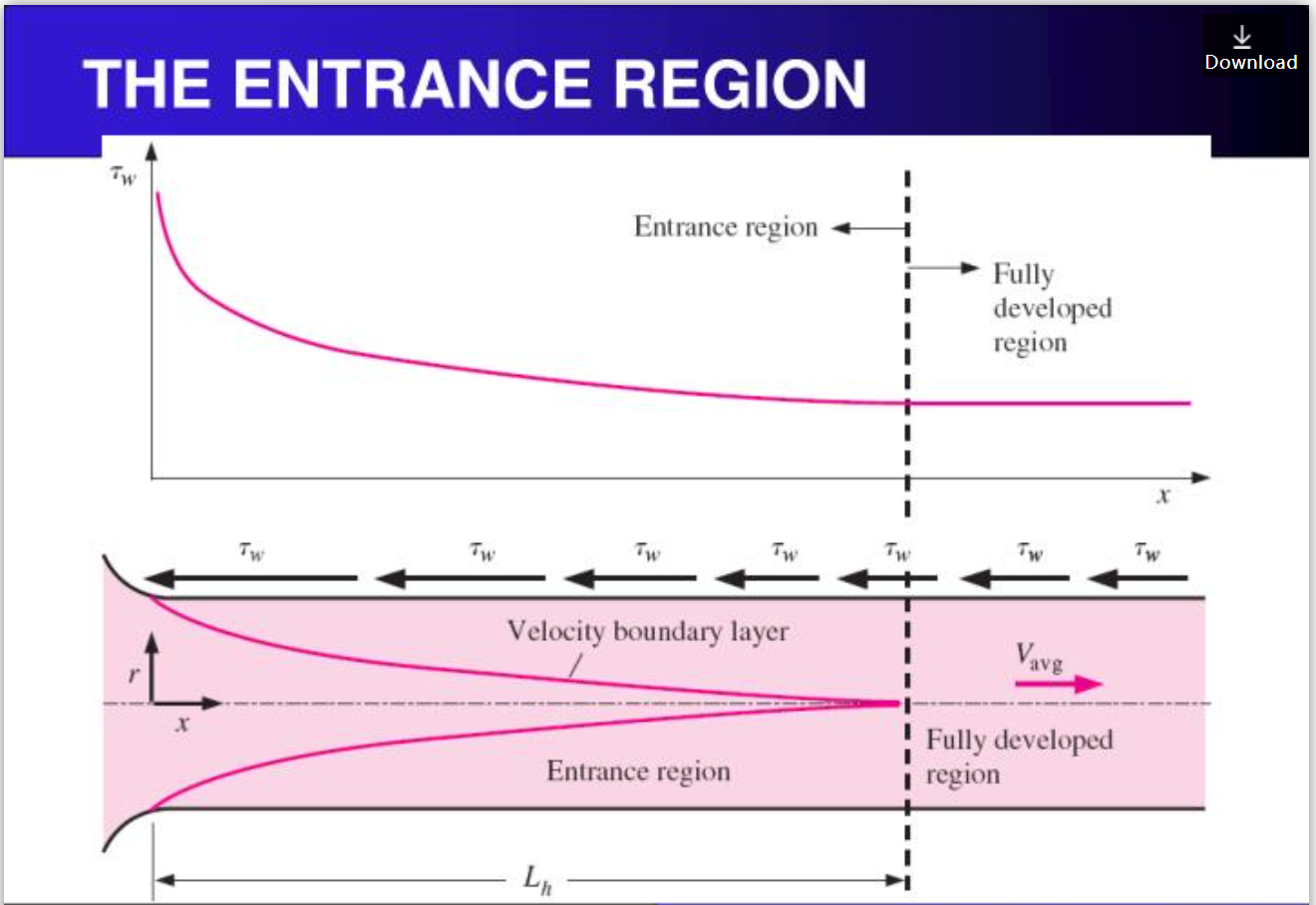
Figure 1.管流发展示意图

对于层流情形，管流的雷洛数低于2300 ，其非充分发展段长度约为115D。而对于湍流情形，其非充分发展段长度约为：

层流管流

获取该案例
结合上述计算域尺度，以及层流的雷洛数范围，本案例的参数如表格 1所示：

表格 1 层流管流案例参数

入口速度	动力粘度	管径D	ReD	管长L
10 m/s	0.01 Pa·s	2m	2000	300m

本案例收敛情况图2所示，在100步左右达到质量收敛准则(1e-5)

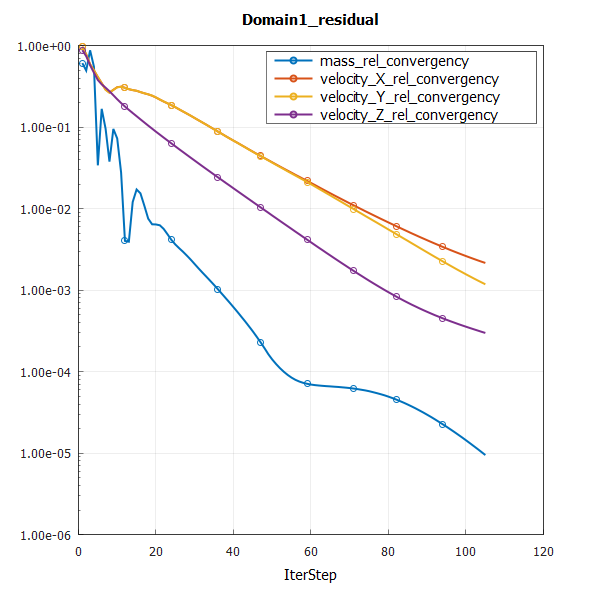
Figure 2.层流管流收敛

Figure3给出了速度分布，可以看出计算尺度内，流动的确完成充分发展。

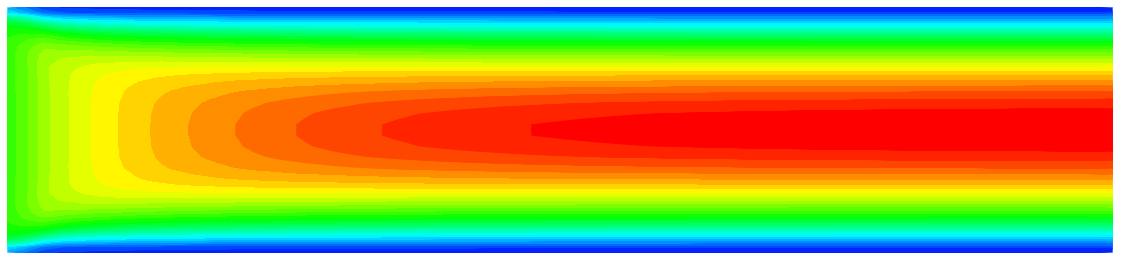
Figure 3.管内速度发展分布，轴向1：30比例缩放

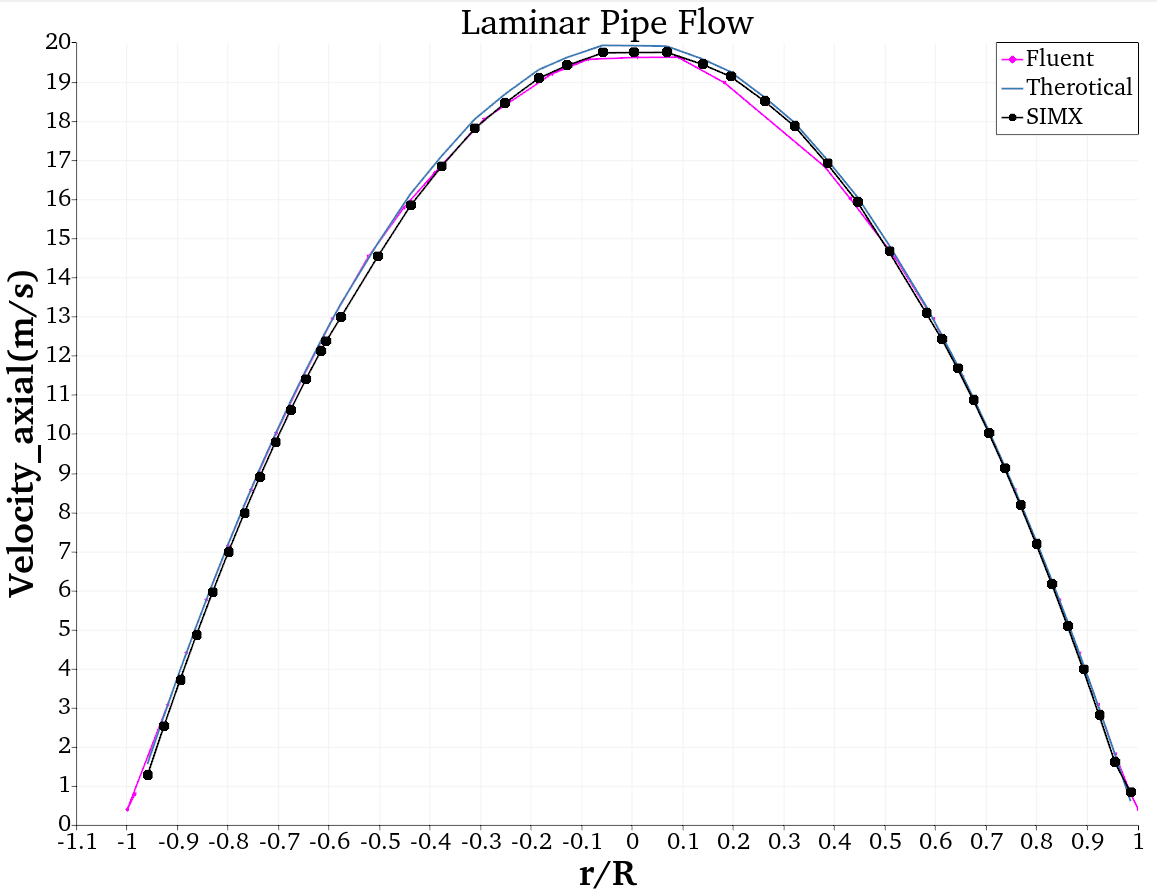
Figure 4.充分发展段速度分布

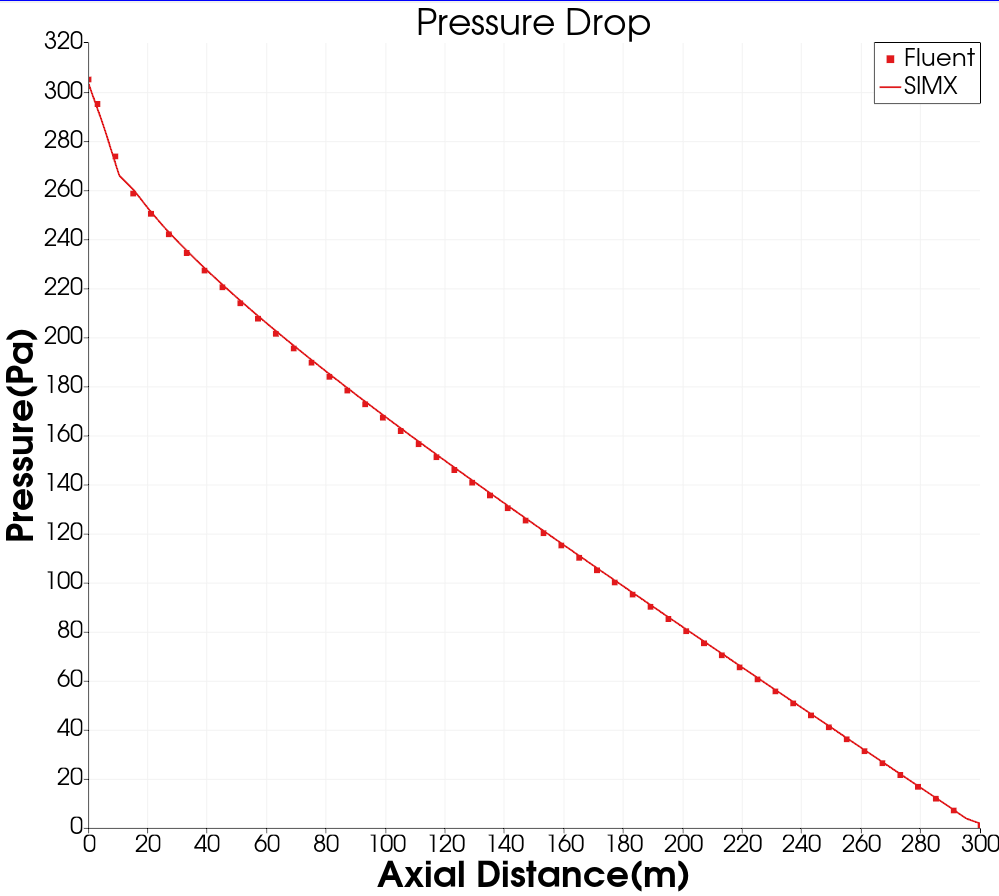
Figure 5.管内压强分布

湍流管流

获取该案例
结合上述计算域尺度，以及湍流雷洛数范围，本案例的参数如表格 2所示：

表格 2 湍流管流案例参数

入口速度	动力粘度	管径D	ReD	管长L	湍流强度
10 m/s	0.0004 Pa·s	2m	50000	60m	1%

同时本案例采用了四套不同的网格，以验证壁面不同网格精度下湍流（以及壁面函数）的计算正确性。

本案例收敛情况图6所示，在150步左右达到质量收敛准则(1e-5)。

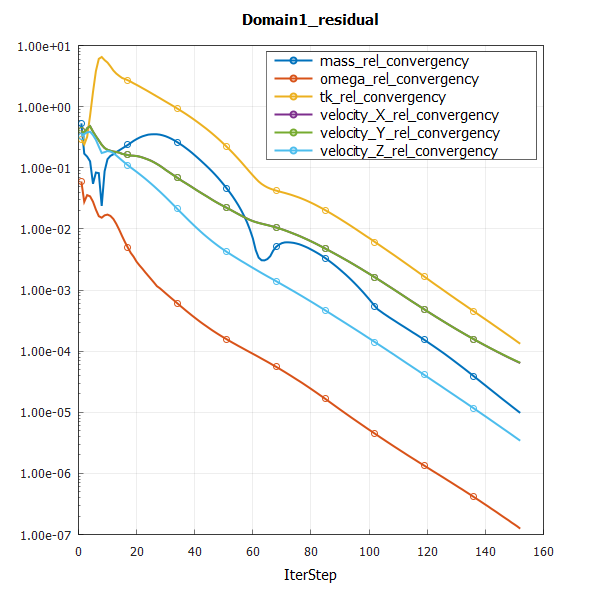
Figure 6.湍流管流收敛

Figure 7.管内速度发展分布，轴向1：5比例缩放

下图给出不同的边界层网格计算给出的速度分布和压强分布，不同网格均能收敛到正确的结果，证明网格适应能力。

Figure 8.充分发展段速度分布

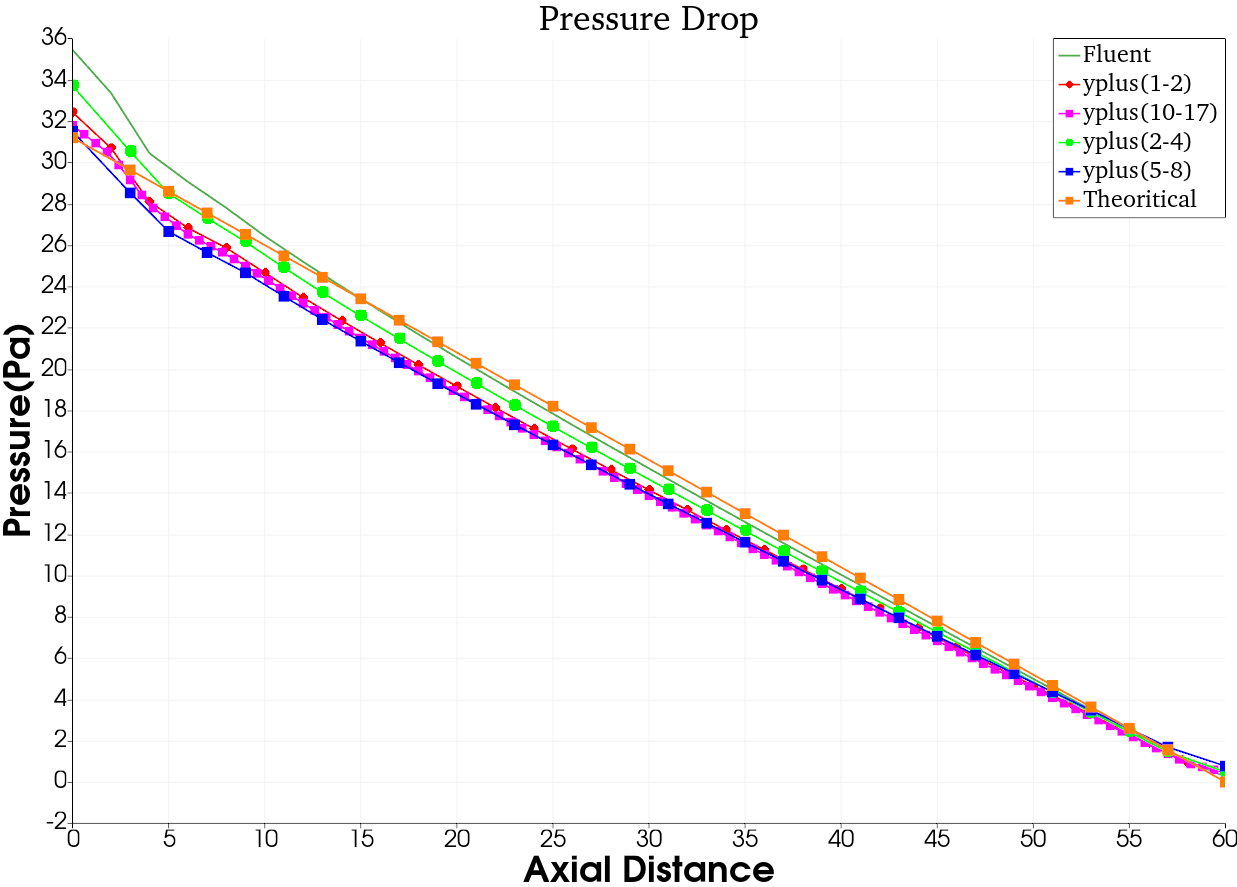
Figure 9.管内压强分布